3384. Диспетчер

В клане ниндзя, ниндзя отправляют к клиенту, и потом они получают вознаграждение в соответствии с их работой.

В клане ниндзя имеется один ниндзя, именуемый Мастером. Каждый ниндзя кроме Мастера имеет ровно одного босса. Чтобы гарантировать конфиденциальность и поощрить лидерство, все инструкции по заданиям всегда передаются боссом своим подчинённым. Другими методами запрещается передавать инструкции.

Вы хотите собрать некоторое количество ниндзя и отправить их к клиенту. Вы должны заплатить каждому из отправленных ниндзя. Для каждого ниндзя зафиксирована оплата. Суммарная плата должна уложится в бюджет. Кроме того, чтобы передавать инструкции отправленным ниндзя, Вы должны выбрать одного ниндзя как менеджера, который сможет посылать инструкции всем им. Ниндзя, который не был выбран, может передавать сообщения. Менеджер не обязательно должен быть отправлен к клиенту. Если менеджер не отправлен, ему не нужно платить.

Вы хотите максимизировать степень удовлетворённости клиента, оставаясь в рамках бюджета. Степень удовлетворённости вычисляется как произведение общего количества отправленных ниндзя и уровня лидерства менеджера. Для каждого ниндзя обозначен его уровень лидерства.

Напишите программу, которая зная для каждого ниндзя его босса b_i, размер оплаты c_i, уровень лидерства l_i (1 ≤ i ≤ n), и размер бюджета m, выведет максимально возможное значение уровня удовлетворённости клиента, при условии, что менеджер и отправленные ниндзя выбраны так, что все условия соблюдены.

Вход. Первая строка содержит количество ниндзя n (1 ≤ n ≤ 10⁵) и бюджет m (1 ≤ m ≤ 10⁹). Следующие n строк описывают босса, зарплату и уровень лидерства каждого ниндзя. (i + 1) - ая строка содержит три целых числа b_i, c_i, l_i (0 ≤ b_i < i, 1 ≤ c_i ≤ m, 1 ≤ l_i ≤ 10⁹), обозначающих босса i-го ниндзя b_i, зарплату i-го ниндзя c_i, и его лидерский уровень l_i. i-ый ниндзя является Мастером, если b_i = 0. Так как всегда соблюдается неравенство b_i < i, то для каждого ниндзя номер его босса всегда меньше номера его самого.

Выход. Выведите максимальное возможное значение уровня удовлетворённости клиента.

Пример входа	Пример выхода
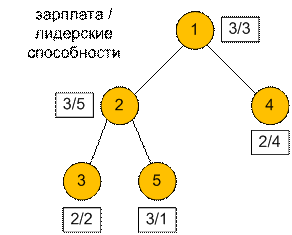
5 4 0 3 3 1 3 5 2 2 2 1 2 4 2 3 1	6

РЕШЕНИЕ

структуры данных - дерево

Анализ алгоритма

Запустим поиск в глубину из вершины 0. Для каждой вершины дерева v построим мультимножество зарплат, находящихся в поддереве с корнем v. Будем, например, хранить такое мультимножество в очереди с приоритетами. Одновременно будем поддерживать значение суммы всех этих зарплат.

Пусть ниндзя v выбран в качестве менеджера. Выгодно отправлять к клиенту тех ниндзя, которые требуют меньшую зарплату. Удаляем из мультимножества наибольшие зарплаты до тех пор, пока сумма оставшихся зарплат не станет меньше или равной бюджету m. Вычисляем удовлетворенность клиента.

Перебираем всех ниндзя в качестве возможных менеджеров, ищем максимальное значение удовлетворенности клиента.

Пример

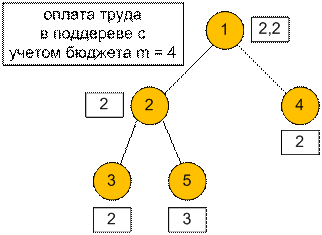
Рассмотрим вершину номер 2. При объединении ее зарплаты с зарплатами ее сыновей получим {2, 3, 3}. Бюджет равен m = 4. Следует произвести оплату тем кто требует меньше всего и помещается в бюджет. Поэтому множество зарплата станет {2}.

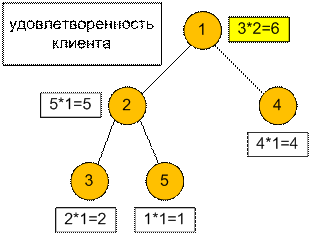
Удовлетворенность клиента считаем в каждой вершине как произведение лидерских качеств ниндзя (менеджера) на количество элементов в оплате труда.

Пусть ниндзя 1 – менеджер. Тогда он отправит к клиенту ниндзя с номерами 3 и 4, заплатив им 2 + 2 = 4, таким образом вложившись в бюджет m = 4. Удовлетворенность клиента равна лидерским способностям менеджера 1, умноженная на количество отправленных к клиентам ниндзя, то есть 3 * 2 = 6.

Реализация алгоритма

Граф храним в g. Объявим массив очередей с приоритетами pq: pq[v] хранит мультимножество зарплат, находящихся в поддереве с корнем v. Значение sum[v] хранит сумму чисел в мультимножестве pq[v].

#define MAX 100010

priority_queue<int> pq[MAX];

vector<vector<int> > g;

int cost[MAX], leader[MAX];

long long sum[MAX];

Поиск в глубину из вершины v. Строим мультимножество pq[v].

void dfs(int v)

{

int i, to;

pq[v].push(cost[v]);

sum[v] += cost[v];

for (i = 0; i < g[v].size(); i++)

{

to = g[v][i];

dfs(to);

Вершина to является сыном v. Занесем все элементы pq[to] в pq[v]. Размер очереди, куда будут переноситься числа, должен быть больше.

if (pq[v].size() < pq[to].size()) swap(pq[v], pq[to]);

Переносим числа в pq[v], одновременно очищая в pq[to] для экономии памяти.

while (pq[to].size() > 0)

{

pq[v].push(pq[to].top());

pq[to].pop();

}

Добавляем к sum[v] сумму чисел мультимножества потомка sum[to].

sum[v] += sum[to];

На вершине очереди находятся большие числа (у нас max - куча). Удаляем их пока сумма чисел в оставшемся мультимножестве не будет превышать бюджет m.

while (sum[v] > m)

{

sum[v] -= pq[v].top();

pq[v].pop();

}

}

res = max(res, leader[v] * (long long)pq[v].size());

}

Основная часть программы. Читаем входной граф.

scanf("%d %d",&n,&m);

g.resize(n+1);

for (i = 1; i <= n; i++)

scanf("%d %d %d",&parent,&cost[i],&leader[i]);

g[parent].push_back(i);

}

Запускаем поиск в глубину из нулевой вершины.

dfs(0);

Выводим результат.

printf("%lld\n", res);